Page126

Monoalphabetic and Polyalphabetic Ciphers

A monoalphabetic cipher uses one alphabet: a specific letter (like “E”) is substituted for another (like “X”). A polyalphabetic cipher uses multiple alphabets: “E” may be substituted for “X” one round, and then “S” the next round.

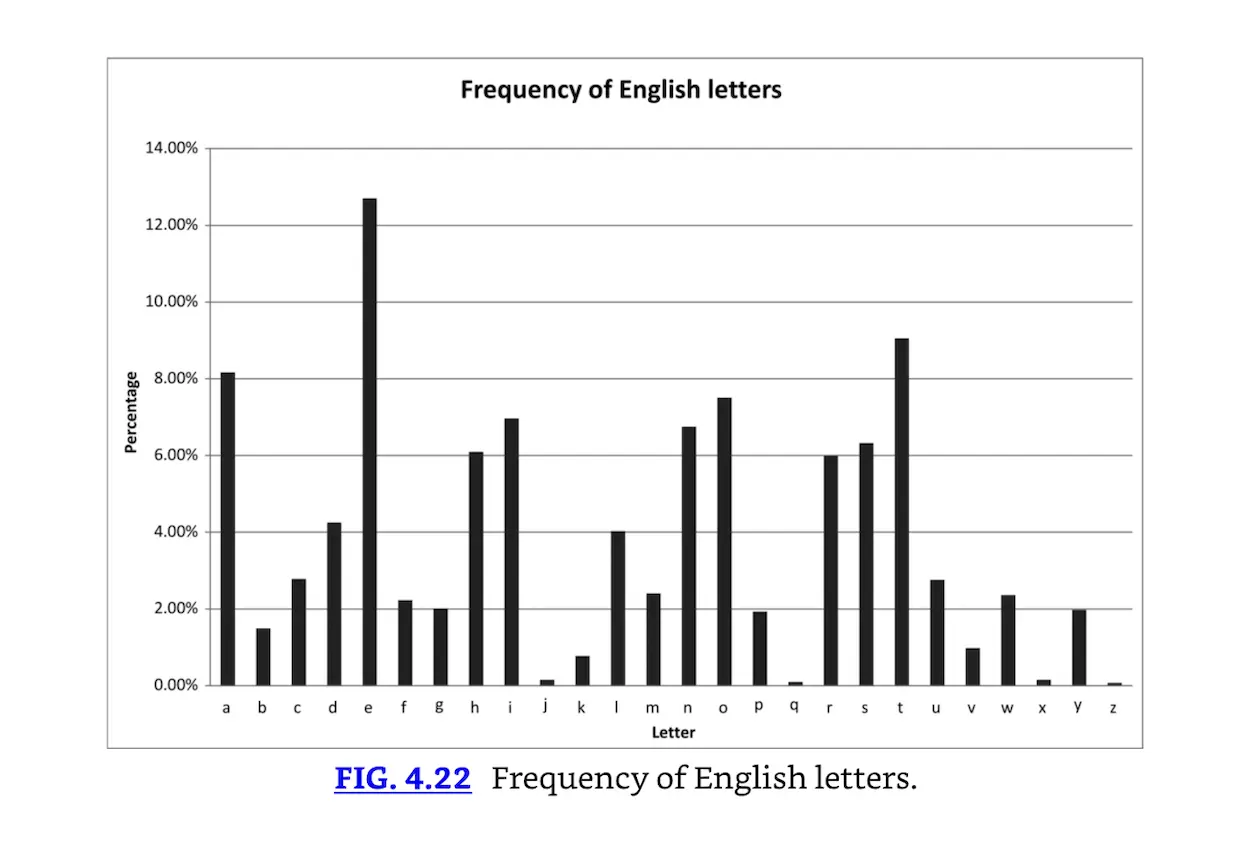
Monoalphabetic ciphers are susceptible to frequency analysis. Fig. 4.22 shows the frequency of English letters in text. A monoalphabetic cipher that substituted “X” for “E,” “C” for “T,” etc., would be quickly broken using frequency analysis. Polyalphabetic ciphers attempt to address this issue via the use of multiple alphabets.

Modular Math

Modular math lies behind much of cryptography: simply put, modular math shows you what remains (the remainder) after division. It is sometimes called “clock math” because we use it to tell time: assuming a 12-hour clock, 6 hours past 9:00 PM is 3:00 AM. In other words, 9 + 6 is 15, divided by 12 leaves a remainder of 3.

As we will see later, methods like the running-key cipher use modular math. There are 26 letters in the English alphabet; adding the letter “Y” (the 25th letter) to “C” (the third letter) equals “B” (the 2nd letter). In other words, 25 + 3 equals 28. 28 divided by 26 leaves a remainder of 2. It is like moving in a circle (such as a clock face): once you hit the letter “Z,” you wrap around back to “A.”

Exclusive Or (XOR)

Exclusive Or (XOR) is the “secret sauce” behind modern encryption. Combining a key with a plaintext via XOR creates a ciphertext. XOR-ing the same key to the ciphertext restores the original plaintext. XOR math is fast and simple, so simple that it was historically implemented with phone relay switches.

Two bits are true (or 1) if one or the other (exclusively, not both) is 1. In other words: if two bits are different, the answer is 1 (true). If two bits are the same, the answer is 0 (false). XOR uses a truth table, shown in Table 4.3. This dictates how to combine the bits of a key and plaintext.

X	Y	X XOR Y
0	0	0
0	1	1
1	0	1
1	1	0

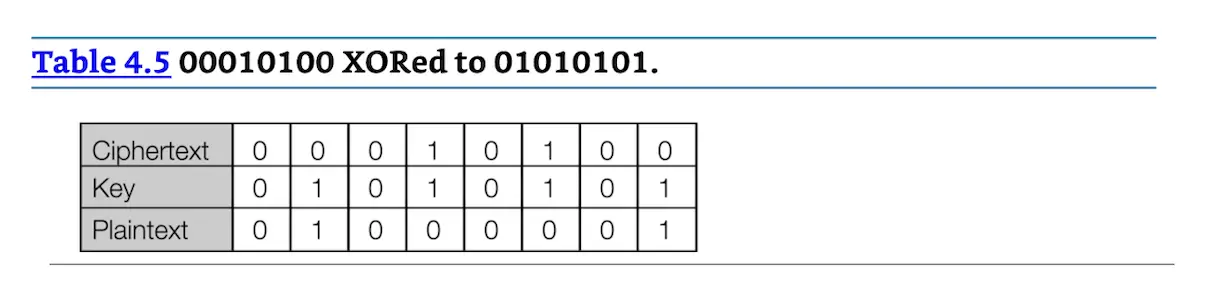
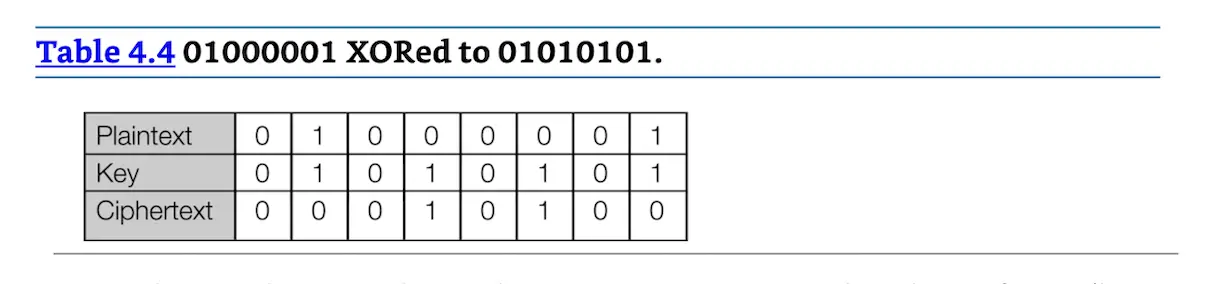
If you were to encrypt the plaintext “ATTACK AT DAWN” with a key of “UNICORN,” you would XOR the bits of each letter together, letter by letter. We will encrypt and then decrypt the first letter to demonstrate XOR math. “A” is binary 01000001 and “U” is binary 01010101. We then XOR each bit of the plaintext to the key, using the truth table in Table 4.3. This results in a ciphertext of 00010100, shown in Table 4.4.

Now let us decrypt the ciphertext 00010100 with a key of “U” (binary 01010101). We XOR each bit of the key (01010101) with the ciphertext (00010100), again using the truth table in Table 4.3. We recover our original plaintext of 01000001 (ASCII “A”), as shown in Table 4.5.